Le risonanze modali (anche dette “modi” o “modi propri”) sono una serie di onde stazionarie causate dalle riflessioni del suono sulle diverse superfici di una stanza. Esistono 3 tipologie di modi: assiali, tangenziali ed obliqui. L’attività modale si sviluppa in maniera direttamente correlata alle dimensioni della stanza.
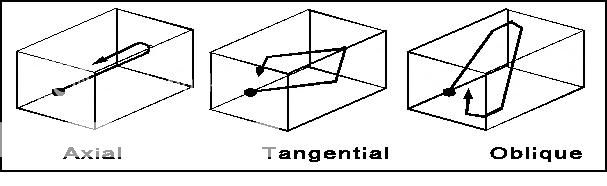
I modi assiali hanno l’impatto maggiore e, molte volte, sono gli unici ad essere considerati.
I modi tangenziali ed obliqui, sebbene abbiano un’influenza minore per singolo modo, si sviluppano in numero maggiore. Pertanto, una combinazione di modi tangenziali ed obliqui può arrivare a causare problemi di entità paragonabile a quelli causati dai modi assiali.
Le risonanze modali sono causa di picchi e nulli (rilievi e avvallamenti) nella risposta in frequenza. Quando 2 o più onde di una certa frequenza si combinano e sono in fase tra loro, si verifica un picco nella risposta in frequenza. Al contrario, quando si combinano in controfase, si cancellano l’una con l’altra e si verifica un nullo (parziale o totale).
Per contrastare l’effetto delle risonanze modali, si interviene assorbendo il più possibile le riflessioni causate da una superficie (ad esempio il muro posteriore), cosicché non vi sia più nulla che possa sommarsi o cancellarsi. Nonostante gli angoli non siano la soluzione definitiva, hanno il vantaggio di essere il vertice di 2 o 3 dimensioni della stanza e per questa ragione sono ottimi candidati per il trattamento. Può capitare però che alcuni problemi modali, per essere risolti, richiedano il trattamento del muro posteriore o addirittura del soffitto e non siano risolvibili con il solo trattamento degli angoli.
La formula di seguito permette di calcolare tutte le risonanze modali (non solo quelle assiali):
F = c/2 * sqrt(p^2/L^2 + q^2/W^2 + r^2/H^2)
F = frequenza
c = velocità del suono (344 metri al secondo)
sqrt = radice quadrata
^2 = elevamento al quadrato
L = lunghezza della stanza
W = larghezza della stanza
H = altezza della stanza
p, q ed r rappresentano i modi che si desidera calcolare. Per il calcolo del modo assiale relativo alla lunghezza della stanza, p=1, q=0, r=0. Per conoscere il secondo modo assiale, p=2, q=0, r=0.
Per calcolare un modo tangenziale, imposta ad 1 una delle variabili. Ad esempio, per calcolare il primo modo tangenziale relativo a lunghezza e larghezza, p=1, q=1, r=0.
In linea generale, man mano che si sale in frequenza con i multipli (armoniche superiori) dei vari modi, essi diventano meno intensi, ma al contempo si manifestano in più posizioni all’interno della stanza.
